Noviembre

Clase N°5

Fecha: Quito, 09 de noviembre del 2016.


Ejercicio

• En una empresa financiera, los empleados disponen de computadoras portátiles de distintas marcas, un resumen de números de máquinas, de acuerdo a su respectiva marca se presenta en el siguiente cuadro.

Marca	Número de respuestas (ni)	fi (%)	Angulo
Toshiba	135	41.4	149
Dell	76	23.3	84
HP	53	16.3	58
Lenovo	43	13.2	48
No sabe	19	5.8	21

       X= Marca de las computadoras portátiles (Cualitativas) 

       Mo= Marca Toshiba

• Diagrama de Barras

 No se utiliza para variables cuantitativas.

 Gráfico N°1

Descripción: El gráfico N° 1 representa las frecuencias relativas de las marcas de computadoras portátiles usadas en una empresa comercial.

Interpretación: En el gráfico N°1 Se evidencia que la marca Toshiba presenta una alta relatividad, mientras que  existe un bajo porcentaje en la opción no sabe

• Diagrama Circular o Sectores:

Para calcular los sectores, se realiza un regla de tres con los porcentajes y los ángulos.

360 → 100%

   x    → 41.4%

Datos agrupados en intervalos o clases

Distribución de frecuencia.

1. Decidir el número de clases o intervalos.
   

   N° Observaciones	N° De Clases Recomendadas
   20-50	6
   51-100	7
   101-200	8
   201-500	9
   501-1000	10
   >1000	11-20

   
   
                k= 1+3.3 log(n)
   donde,  k: N° de clases o intervalos

                  n: N° de observaciones
2. Calcular la longitud de la clase (A)
   
   
   
3. Construir las clases o intervalos.
4. Calcular las columnas de la tabla de frecuencias.
   
   Intervalos: [Linf1 - Lsup [
   
   Marca de clase: mi = (intervalo)/2
   
   Frecuencia: n1, n2, ...
   
   Frecuencia Relativa: f1= (n1/n)
   
   Frecuencia acumulada: Ni= ni + ni-1
   
   Frecuencia relativa Acumulada: Fi= fi+fi-1

Ejemplo: Video

Clase N°6

Fecha:Quito, 11 de noviembre del 2016.

En esta clase se realzaron ejercicios.
Ejemplo.

Clase N°7

Fecha:Quito, 16 de noviembre del 2016.

En esta clase se realizó la actividad de el Corazón.  Disponible en Taller 1.

Clase N°8

Fecha:Quito, 18 de noviembre del 2016.

Muestras Bivariadas

Dos variables para la misma muestra.
Ej: Peso- Estatura, Calificaciones Examen Parcial- Examen final.

i) Identificar variables, "x" y "y".

ii) Diagrama de dispersión.

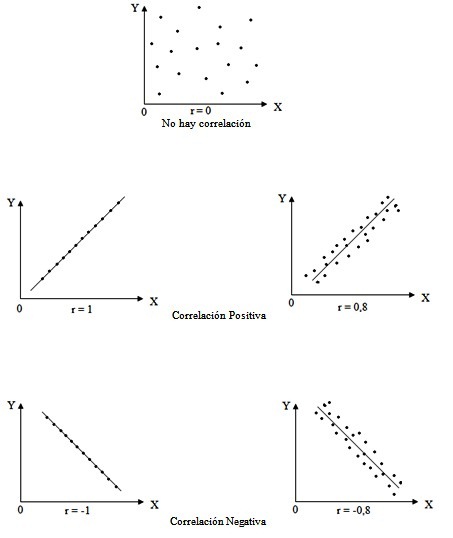
Correlación

Covarianza Muestral

Sean  

x, y: variables muestrales 

n: tamaño de la muestra

X(media), Y(media): medias muestrales

Sx² , Sy²: Varianzas muestrales.

Sxy: covarianza muestra.

La covarianza es una medida de la correlación entre las variables.

Si Sxy > 0 → la tendencia es lineal positiva

Si Sxy < 0 → la tendencia es lineal negativa

Coeficiente de correlación (r) 

-1 ≤ r ≤ 1

r		x ^ y
Cercano a 1 Cercano a -1 Cercano a 0	→  →  →	Correlación lineal positiva fuerte. Correlación lineal negativa fuerte. Correlación lineal muy débil o no están correlacionados linealmente.

Matriz de Varianza-Covarianza

Matriz de Correlación

Más información 

Clase N°9

Fecha:Quito, 19 de noviembre del 2016.

Se realizó la Evaluación 1. Corrección: Tarea 4, Corrección de la Evaluación 2

Clase N°10

Fecha:Quito, 23 de noviembre del 2016

Probabilidad

Medida cuantitativa de qué tan probable es que  ocurra o no un evento.

Experimento: Proceso con un resultado que no se puede predecir certeramente con anterioridad.

Espacio Muestral: Conjunto de posibles resultados.

Evento: Subconjunto del espacio muestral.

Dado un experimento y cualquier evento A:
 - P(A) denota la probabilidad de que ocurra el evento A.
 - P(A) constituye la proporción de veces que se presenta el evento A en el tiempo, si es que el experimento se realizara una y otra vez.

Vea ejemplos aquí.

Probabilidad es una medida aproximada.
Axiomas de la probabilidad

1. Si la probabilidad es 1, es un evento cierto y si es 0 (cero) es imposible.
2. Para cualquier evento A  0  ≤ P(A)  ≤  1
3. Si A y B son eventos mutuamente excluyentes, entonces P(A⋃B) = P(A) + P(B). De forma general, si A1, A2... son eventos mutuamente excluyentes, en tonces P(A1⋃A2⋃....)=

Sean A y B cualesquiera eventos, entonces P(A ⋃B) =P(A) + P(B) - P(A B)

Diagrama de árbol.

Es un mecanismo utilizado para enumerar todos los resultados posibles de una secuencia        de experimentos o eventos donde a cada evento puede ocurrir en un número finito de formas.

  

Se recomienda ver el siguiente video.
https://www.youtube.com/watch?v=FCIxoxCUCGc


Clase N°11

Fecha:Quito, 25 de noviembre del 2016

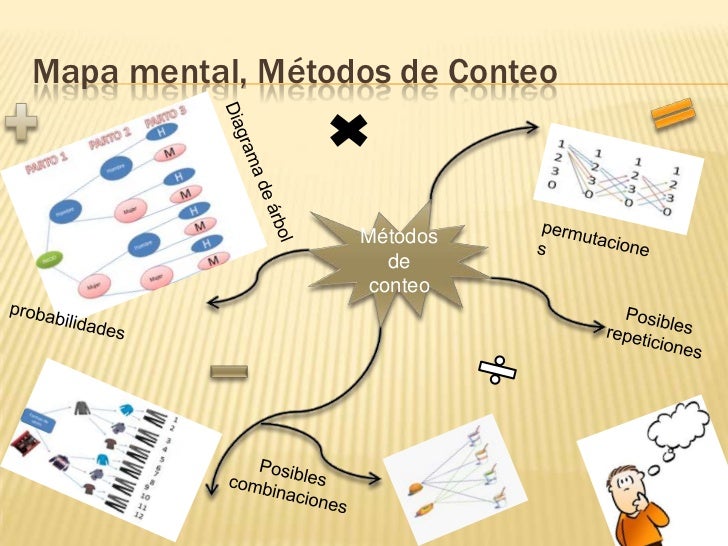
MÉTODOS DE CONTEO

Principio fundamental

Si una operación se puede realizar de n maneras y si para cada una de esas n maneras  se puede realizar una segunda operación de n2 maneras Entonces el número total de manera se realizan dos operaciones es: n1 * n2

Ejemplo:

• Cierto tipo de automóvil se encuentra disponible en tres colores: rojo, azul o verde, y puede tener un motor grande o pequeño. ¿De cuántas maneras puede un comprador elegir un automóvil?

Tamaño del motor:  n1= 2 

Color del automovil: n2 =3

n1 * n2= (2) (3) = 6

→ Número total de maneras de elegir = 6 

Permutaciones

- Es un ordenamiento de un conjunto de n elementos.

- El número de permutaciones de n elementos es n!

  n!= n(n l)(n 2) . . . (3)(2)(1).

*0!= 1.

Ejemplo:

• Cinco personas están en la hilera de un cine. ¿En cuántas maneras diferentes se pueden ordenar?
  5! = (5)(4)(3)(2)(1) 120

Permutaciones de k elementos

- El número de permutaciones de k elementos de un total de n elementos es:

Más información

Clase N°12

Fecha:Quito, 30 de noviembre del 2016

Ejercicio

• En una habitación se encuentra el siguiente grupo de personas: 5 hombres mayores de 21, 4 menores de 21, 6 mujeres mayores de 21, 3 mujeres menores de 21. Se elige una persona al azar y se definen los siguientes sucesos: 

         A: La persona es mayor de 21.

         B: La persona es menor de 21.

         C: La persona es hombre.

         D: La persona es mujer.

      Evaluar las siguientes probabilidades:

         a)  P(B⋃D)

         b)  P(A⋃C)

         c)  P(A^c⋃B^c)

Experimento: Selección de una persona de una habitación.

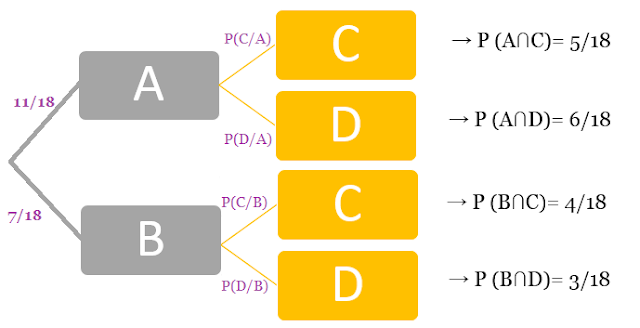
Tabla de doble entrada

	A	B	Total
C	5	4	9
D	6	3	9
Total	11	7	18

a) P(B) = 7/18                      P(D) = 9/18                          P(B∩D) = 3/18

P(B⋃D) = P(B) + P(D) - P(B∩D) = 7/18 + 9/18 - 3/18 = 13/18

   

b) P(A) = 11/18                   P(C) = 9/18                          P(A∩C) = 5/18

     P(A⋃C) = 11/18 + 9/18 - 5/18 = 15/18

            

c) P(A^c) = 7/11                    P(B^c) = 11/18                       P(A^c∩B^c) = 0

     P(A^c⋃B^c) = 7/11 + 11/18 - 0 =1

                        

d) P(A/C) = P(A∩C)/P(C) = 5/9

e) P(C/A) =  P(A∩C)/P(A) = 5/11 

Diagrama de árbol:

*Para más ejercicios revisa los libros recomendados en este blog debajo de datos personales.
O puedes ver otro ejemplo en un vídeo