Octubre

PRIMER BIMESTRE

Clase 1

Fecha: Quito, 12 de octubre del 2016.


INTRODUCCIÓN

Se inició la materia de probabilidad y estadística básica 2016-B.

Se proporcionaron indicaciones generales para el desenvolvimiento apropiado de la clase, en las cuales la Ing. Mónica Mantilla explicó su forma de trabajo, la importancia de los valores en clase y su forma de evaluación.

Como primera tarea sencilla se mandó a crear este blog y a configurarlo según las instrucciones.

Expuestas en: https://sites.google.com/site/probabilidadyestadistica2016b/portafolio-estudiantil-ing-ambiental

Indicaciones Iniciales:

►Valores:

¨       Respeto

¨       responsabilidad

¨       solidaridad

¨       compañerismo

¨       honestidad.

Trabajar con estos valores dará un ambiente de aprendizaje correcto, nos hará ser mejores personas y por ende buenos profesionales.

►Actividades y Tareas:

¨       Crear una carpeta en google-drive con el nombre de tareas junto al nombre del estudiante, y compartirla con la catedrática para que las tareas calificadas que subamos sean una evidencia de nuestro trabajo en el semestre.

¨       Las tareas presentadas deben tener el formato de encabezado en papel boon expuesto por la ingeniera, para poder llevar las tareas claras y ordenas

¨       El portafolio estudiantil, es una forma de repasar la materia impartida en clase, ya que se debe hacer un breve resumen de los temas dados en clase también debe incluirse la carpeta de tareas en este portafolio.

► Evaluación:

    Se dio a conocer los puntajes que tendrá cada actividad en clase incluyendo exámenes y pruebas.

Tareas, actividades, portafolio	20%
Evaluación 1	20%
Evaluación 2	20%
Examen	40%

Clase 2

Fecha: Quito, 14 de octubre del 2016.

MUESTREO

"Es un proceso que nos permite la extradición de una muestra a partir de una población." (Salto Isbel)

Introducción.

Estadística:

►Descripción → Descripción de los datos obtenidos de la muestra. 

► Inferencia  → Partir de una serie de hipótesis se llegue a una variable. 

1. Descripción de datos
2. Análisis de muestras
3. Medición de relaciones 
4. Predicciones (probabilidad) 

Definición básicas.

• Unidad muestral → Individuo.
• Muestra es un subconjunto de la población debe ser un conjunto representativo de la población.
• Población o universo → Total de individuos de estudio.

http://www.universoformulas.com/estadistica/inferencia/muestreo-no-probabilistico/

Tipos de datos.

• Numéricos (Cuantitativas)

          1. Discretos (conteos)  → Número de hijos.

                                            → Número de facturas.

                                            → Número de vehículos.

          2. Continuos (Decimal) → Peso (kg, lb, g, etc.)

                                            → Estatura (m, cm, pies, etc.)

                                            → Temperatura (°C, °F, °K, etc.)

                                            → Ventas ($, €, £, etc.)

• Categóricos (Cualitativos)

         → Clases económicas.

         → Estudios.

         → Genero

         → Estado civil.

         → Grupo étnico.

Escalas de medición.

• Nominal → Datos pueden ser representativos
• Ordinal → Orden (creciente, decreciente)
• De intervalo → Todas las variables que están en un intervalo (fracciones, decimales, etc.)
• De razón → Si es que esa escala tiene cero absoluto.

Datos atípicos.

Referente a datos inusuales, que tal vez estén fuera del rango.

Un valor atípico es una observación extrañamente grande o pequeña. Los valores atípicos pueden tener un efecto desproporcionado en los resultados estadísticos, como la media, lo que puede conducir a interpretaciones engañosas.

Para más información:

https://youtu.be/6JUIRzs6P9Y

Referencia:

• SALTO, Isbel. "Tema 13. Inferencia estadística Principales conceptos. Muestreo. Distribución muestral de un estadístico. Principales distribuciones muestrales." 2014 [fecha de consulta: 16 Octubre 216]. Disponible en; <http://slideplayer.es/slide/106350/

Clase 3

Fecha: Quito, 26 de octubre del 2016.

Resumen Estadístico

• Es una serie de cantidades calculadas.
• Se pretende describir las características de los individuos de la muestra.
• Las principales o más comunes son:

Media o promedio y desviación estándar

• La media indica el cerebro de los datos.
• La desviación estándar indica la distribución de datos.
• La media se calcula:

 ; n es el tamaño de la muestra.

Toda gráfica debe tener: Título. Numeración. Título de los ejes. Escalas adecuadas en los ejes. Descripción del gráfico. Interpretación del gráfico.

La desviación estándar muestral

Mide el grado de dispersión de una muestra, o sea,  cuanto tienden a alejarse los valores de la muestra  de su media.

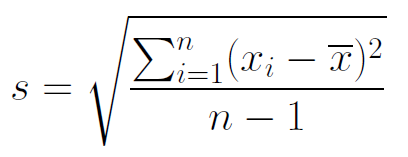
La varianza muestral

Promedio de las desviaciones al cuadrado.

Ejemplo:

Un médico de un instituto quiere realizar un estudio para ver si los alumnos de un centro tienen sobrepeso. Le interesaría calcular la varianza para ver como difieren los pesos respecto a la media. Para ello, se selecciona una muestra de doce alumnos de 14 o 15 años.

Se calcula la media de los pesos de los alumnos, y se obtiene que x = 53,5kg.

Una vez se sabe la media, se halla la diferencia de cada elemento respecto a esta, para calcular la dispersión de los datos.

Una vez se ha calculado el cuadrado de la diferencia de cada elemento con la media, ya se puede determinar la varianza (S2):

El valor alto de la varianza confirma una de sus características: que es sensible a los valores que se separan bastante de la media.

A continación se puede observar un gráfico de las diferencias del peso de cada alumno respecto a la media:

 Mediana muestral

Representa una medida de tendencia central de los datos. 

Para calcular la mediana de una muestra: 

- Ordene los valores del más pequeño al más grande.

- La mediana es el número ubicado en el medio.

Si el tamaño de la muestra es un número par, se acostumbra tomar a la mediana muestral como el promedio de los dos números de en medio.

Mediana recortada

Medida de tendencia central que se diseñó para que no esté afectada por datos atípicos. La media recortada se calcula al arreglar los valores de la muestra en orden, "recortar" un número igual a partir de cada extremo y calcular la media de los restantes.

 

 

Referencias:

- Navidi, W. Resumen Estadístico. Estadística para ingenieros y Científicos. Ed. Mc Graw Hill, S.A, México, 1era ed, 2006, p.p 12-18

- Universo Formulario, Varianza. Disponible en: <http://www.universoformulas.com/estadistica/descriptiva/varianza/>

Clase 4

Moda (Mo)

• Es el valor que más se repite o que tiene una mayor frecuencia en el conjunto de datos.
• Un conjunto de datos puede tener uno o más modas.

Rango (Rg)

• Es la diferencia entre el valor máximo y el valor mínimo.

Percentiles (Pk)

• Son cada uno de los 99 valor es que divide  el rango en 100 partes iguales.


• ……. 1%
• ……. 25%
• ……. 20%
• Quintiles

Q1=P20 Q2= P50= Mediana Q3 = P75

》Cálculo de los percentiles:

• Para datos individuales.

Pk: Xt+Xt+1/ 2          → r= 0

Pk: Xt+1                      → r > 0

t: Parte fraccionaria de la expresión nk/100

r: Parte fraccionaria de la expresión

k: Orden del percentil

Diagrama de cajas o bigotes.

Datos

Xmin, Xmáx

Q1, Q2, Q3

Características de los datos:

Localización	Mediana, media, moda.
Dispersión	Rango, varianza, desviación, rango intercuartil,
Simetría	Consistente de simetría, c. de Puntamiento