Clase N°11
Fecha: Quito, 01 de febrero del 2017Distribución de Muestra
N: Tamaño de la población
n: Tamaño de la muestra
Definición: A la ley de probabilidad que sigue un
estadístico se le denomina DISTRIBUCIÓN DE MUESTREO
- Distribución de muestreo de la muestra
Suponemos que se tiene una muestra X1, X2,...;Xn
de una población que tiene media μ y varianza σ2. A
partir de una muestra calculamos el promedio (x media), entonces:
Esta aplicación es válida para n ≥ 25
- Teorema del Límite Central (T.L.C.)
Ejemplo:
- Distribución de
muestreo de la proporción
Supongamos que se tiene una muestra aleatoria X1,
X2,...,Xn proveniente de una población q sigue una ley
Bernoulli Be(p), definimos:
Donde Xi con probabilidad p y Xi= 0 con
probabilidad 1-p=q, i= 1,2,3
.... n entonces y cuenta el número de n éxitos en n intervalos.
- - La proporción de éxitos en la muestra es:
- La variable aleatoria Y ̴ Bi (n,p)
Se cumple:
n ≥ 25 por el TCL, por tanto :
Te recomiendo ver el siguiente vídeo:
Clase N°12
Fecha: Quito, 03 de febrero del 2017
No se asistió a clases por permiso de facultad.
Clase N°13
Fecha: Quito, 08 de febrero del 2017
- Distribución de muestreo de varianza
- Ley de distribución x^2 (ji cuadrado)Sean X1,X2,X3,....Xn variables aleatorias independientes que siguen una distribución normal estándar, la variable aleatoria T definida:
sigue una distribución X^2 con (n-1) grados de libertad, denotado por:
Grados de libertad=n-1=df=V=gl=q
- Esta distribución esta definida para números positivos.
*Para leer los valores tabulados (ji cuadrado):
1. Escoja los df en la columna izquierda.
2. Considere el nivel de significancia α en la primera fila.
3. Localiza el valor de la ji cuadrado en la tabla. ☺
Te recomiendo ver el siguiente vídeo:
- Ley de distribución de s^2
Supongamos que tenemos una muestra X1,X2,X3,....Xn de una población que sigue una N(μ, σ2) . A partir de la muestra calculamos la varianza muestral.
Se cumple:
1. E(s^2)= σ2
2. V(s^2)= [(n-1) * s^2]/ σ2
3. Xα2 = (n-1) s2/ σ2
¿Deseas saber más?, te recomiendo el siguiente video:
Estimación por intervalos
El intervalo de confianza (IC) es un rango de valores, calculado a partir de los datos muestrales.- A cada intervalo de confianza se le asocia un a probabilidad (1-α) de que contenga el valor del parámetro θ (población) que se pretenda estimar, (1-α)100%; nivel de confianza.
Los valores más usados para (1-α)100% son:

(Pruebas piloto)
(tesis)
(investigaciones de alto nivel)
- El nivel de confianza nos estaría dando la probabilidad de no encontrar al parámetro en el intervalo calculado:
P(LIC ≤ θ ≤ LSC)= (1-α)
donde:
θ: Parámetro de interés
LIC: Limite inferior del intervalo de confianza
LSC: Limite superior del intervalo de confianza
i) MUESTRAS GRANDES
; (1-α)100% ; σ conocida
Te recomiendo ver el siguiente vídeo:
Clase N°14
Si tenemos una muestra de tamaño "n" proveniente de una ley Bermoulli, cuyo parametro "p"(probabilidad de éxito) deseamos estimar.
 Donde:
Donde:
;probabilidad estimada= número de éxitos
nro. de pruebas realizadas
Es el valor Z que le corresponde a α/2
Si E= |p^- p|error en la estimación de la proporción, entonces
*Si no se conoce una estimación de p, por ser una primera investigación. Se asume una probabilidad de estimación igual a 0.5, ya que esta proporcionará el tamaño máximo de la muestra.
Te recomiendo ver el siguiente vídeo:
- Un intervalo de confianza (IC) para la varianza poblacional σ^2, a un nivel de confianza (1-α)100% esta dado por:

;(1-α)100%
Donde:
s^2: Varianza muestral
n-1: grados de libertad
se encuentra en la tabla
ii) MUESTRAS PEQUEÑAS
-Intervalo de confianza de la media poblacional
Donde:
X(media): Media muestral
s: desviación estándar muestral
n: tamaño de la muestra
-Distribución t-Student

La distribución t-Student sirve para estimar la media poblacional normal cuando la muestra es pequeña.
Valor e la distribución t-Student con (n-1) grados de libertad que deja a su derecha una probabilidad α/2
Observaciones
1. Si n ≥ 30, se usa tabla normal.
2. Si n < 30, se usa tabla de distribución t-Student.
3. Si, el valor buscado no está en la tabla se realiza interpolación lineal.
4. Si existen datos atípicos no se usa t-student.
Te recomiendo ver el siguiente vídeo:
Clase N°15
Fecha: Quito, 15 de febrero del 2017
En esta clase realizamos ejercicios de repaso para la prueba y el examen, también realizamos un taller, el cuál estará disponible en evidencias.
Puedes ver ejercicios resueltos aquí y aquí.
☺
Clase N°16
INTERVALO DE CONFIANZA
i) MUESTRAS GRANDES
Estimación de la media poblacional μ
IC:
; (1-α)100% ; σ conocida
Te recomiendo ver el siguiente vídeo:
Clase N°14
Fecha: Quito, 10 de febrero del 2017
Intervalo de confianza para la proporción
Si tenemos una muestra de tamaño "n" proveniente de una ley Bermoulli, cuyo parametro "p"(probabilidad de éxito) deseamos estimar. Donde:
Donde:;probabilidad estimada= número de éxitos
nro. de pruebas realizadas
Es el valor Z que le corresponde a α/2
Despejando n de (1):
*Si no se conoce una estimación de p, por ser una primera investigación. Se asume una probabilidad de estimación igual a 0.5, ya que esta proporcionará el tamaño máximo de la muestra.
Te recomiendo ver el siguiente vídeo:
Intervalo de confianza para la varianza
- Si se desea estimar la varianza de una conjunto de "n" mediciones que suponemos vienen de una ley normal.- Un intervalo de confianza (IC) para la varianza poblacional σ^2, a un nivel de confianza (1-α)100% esta dado por:

;(1-α)100%
Donde:
s^2: Varianza muestral
n-1: grados de libertad
se encuentra en la tabla
Te recomiendo ver el siguiente vídeo:
ii) MUESTRAS PEQUEÑAS
-Intervalo de confianza de la media poblacional
Donde:
X(media): Media muestral
s: desviación estándar muestral
n: tamaño de la muestra
-Distribución t-Student

La distribución t-Student sirve para estimar la media poblacional normal cuando la muestra es pequeña.
Valor e la distribución t-Student con (n-1) grados de libertad que deja a su derecha una probabilidad α/2
Observaciones
1. Si n ≥ 30, se usa tabla normal.
2. Si n < 30, se usa tabla de distribución t-Student.
3. Si, el valor buscado no está en la tabla se realiza interpolación lineal.
4. Si existen datos atípicos no se usa t-student.
Te recomiendo ver el siguiente vídeo:
Clase N°15
Fecha: Quito, 15 de febrero del 2017
En esta clase realizamos ejercicios de repaso para la prueba y el examen, también realizamos un taller, el cuál estará disponible en evidencias.
Puedes ver ejercicios resueltos aquí y aquí.
☺
Clase N°16
Fecha: Quito, 17 de febrero del 2017










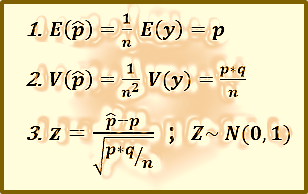















No hay comentarios:
Publicar un comentario